Group 4   (desmond turner, jake shaw, jordan watkins)

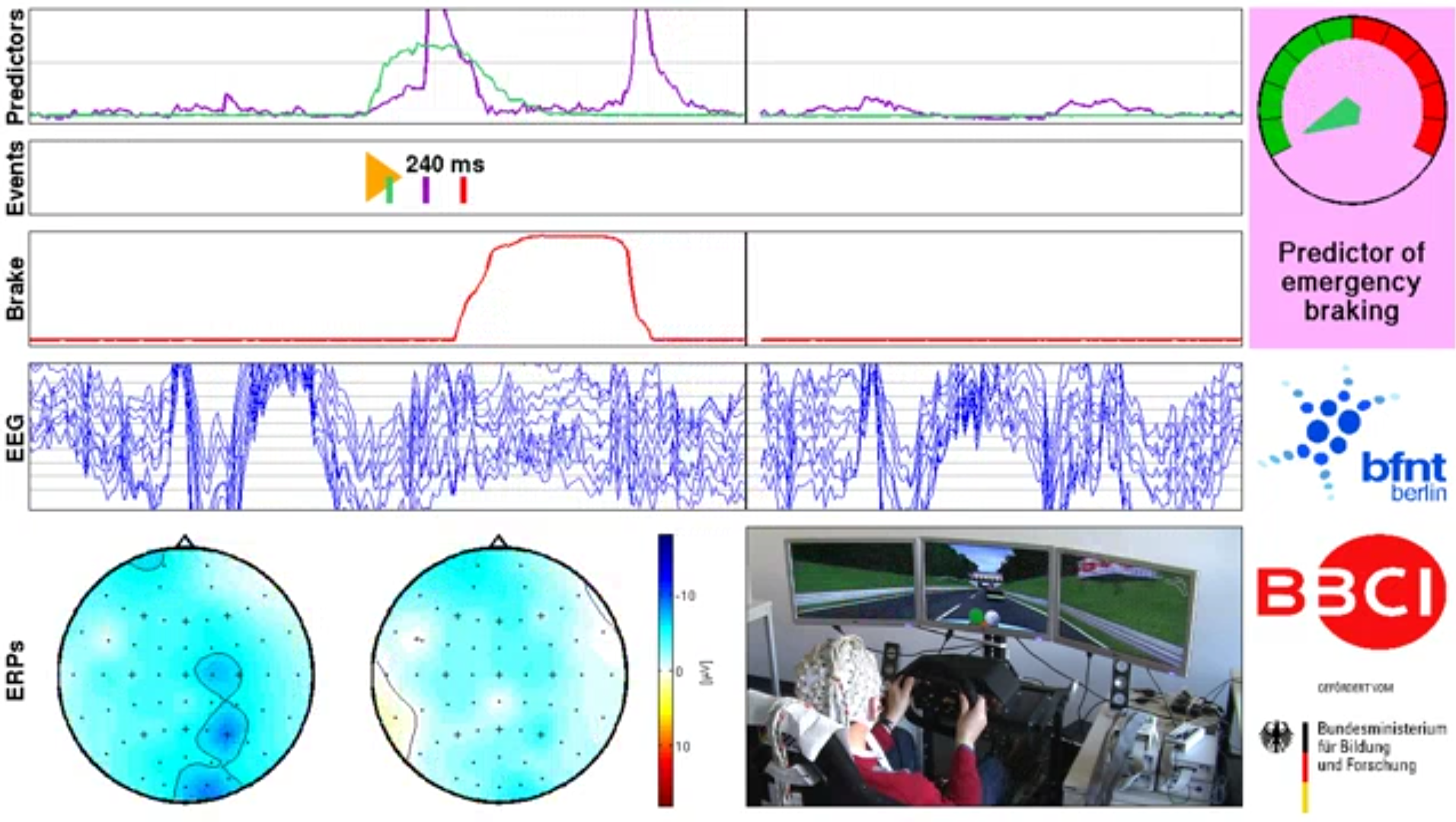
Emergency braking intention detector, Stefan Haufe et al 2011 J. Neural Eng. 8 056001

Approach & Algorithm

As mentioned above, researchers provided a multitude of events within the dataset and the timestamps at which these happen. These events are listed as such: car_brake, car_hold, car_accelerate, car_collision, and react_emg. The first four events are in reference to what the lead car is currently doing at any given point in time, and the fifth is the point in which the driving subject reacts to the lead car braking. Upon this realization, we knew the next task at hand was to solve the problem of aligning the occurrence of all events with the samples of EEG data.

The initial implementation of pulling data around the time of events is shown below. We had chosen the arbitrary value of 500 milliseconds to pull from EEG data, 250 milliseconds before and 250 milliseconds after the event, figuring it would be a sufficient amount of time for the driver to react to the lead car braking. Though, despite this assumption, our classifier was unable to correctly identify when the user braking. We figured we were on the right tracks but our algorithm simply needed some slight refining.

adjustedtime = data{j,1}.mrk.time ./ 5; %mrk.time is in miliseconds, cnt.x samples once every 5 miliseconds
samplerate = ones(cntsize,1); %samplerate vector to hold milisecond intervals
for q = 2:cntsize
	samplerate(q) = samplerate(q-1)+5; %add 5 milisecond more to each index than the previous iteration
end
...
%grab 500ms of eeg data around event
for k = 1:numevents
	if data{j,1}.mrk.y(5,k) == 1 %event 5 is react_emg
            time = adjustedtime(k); %time at which the event occurs
            [~, idx] = min(abs(samplerate-time)); %find closest occurrence of the event in the cnt.x via the samplerate vector
            emgeeg = [emgeeg;data{j,1}.cnt.x(idx-50:idx+50,1:62)]; %grab eeg data within duration
            emgevents = [emgevents;data{j,1}.cnt.x(idx-50:idx+50,63:69)]; %grab event occurrences within duration

Upon further inspection of the documentation of the initial research, we had realized that the occurrence of the driver's reaction to an emergency braking event in the EEG data happens approximately 1300 milliseconds before and 200 milliseconds after the event. The code below reflects this adjustment.

adjustedtime = data{i,1}.mrk.time ./ 5; %mrk.time is in milliseconds, cnt.x samples once every 5 milliseconds
numSkips = 10; %increase to downsample, decrease to upsample
srd = 5; %divisible amount to account for sample rate. For a rate of 200 it would be 5
...
%add label to corresponding raw data
for j = 1:numEvents
	if data{i,1}.mrk.y(5,j) == 1 %event 5 is react_emg
		approx_index = round(adjustedTime(j)/numSkips); 
		for k = approx_index-round((1300/srd)/numSkips):approx_index+round((200/srd)/numSkips) %-1300 ms and +200 ms
                	altered_data(k,numEEG+2) = 1; %label as braking
		end
	end
end

Now that we had the correct amount of EEG signal extracted from each event, and each event labeled respectively, the final step before classifying was extracting our desired features. After experimenting with a wide variety, the five we settled on were mean, standard deviation, activity, mobility, and complexity. The code for extracting each is shown below.

ADwindow = altered_data(m:m+targetSize,1:numEEG);
%mean
features(itr,1:numEEG) = mean(ADwindow);       
%standard deviation
features(itr,numEEG+1:2*numEEG) = std(ADwindow); 
%activity
features(itr,2*numEEG+1:3*numEEG) = var(ADwindow); 
%mobility and complexity
for d = 1:numEEG
	ADwd0 = ADwindow(:,d);
	ADwd1 = zeros(1,length(ADwd0));
	ADwd2 = zeros(1,length(ADwd0));
	for d1 = 2:length(ADwd0)
		ADwd1(d1) = ADwd0(d1) - ADwd0(d1-1);
	end
	%mobility
	features(itr,3*numEEG+d) = std(ADwd1)/std(ADwd0); 
	for d2=3:length(ADwd0)
		ADwd2(d2) = ADwd0(d2) - 2*ADwd0(d2-1) + ADwd0(d2-2);
	end
	FF = (std(ADwd2)/std(ADwd1))/(std(ADwd1)/std(ADwd0));
	%complexity
	features(itr,4*numEEG+d) = FF;
end              

Results

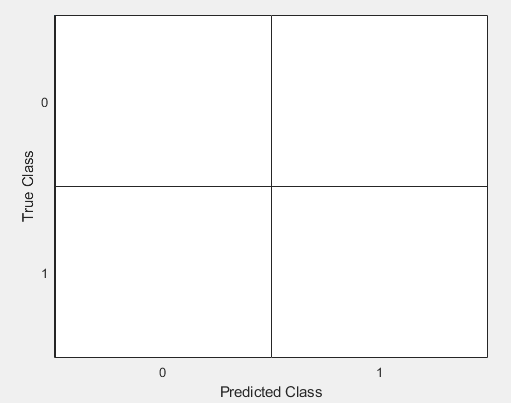
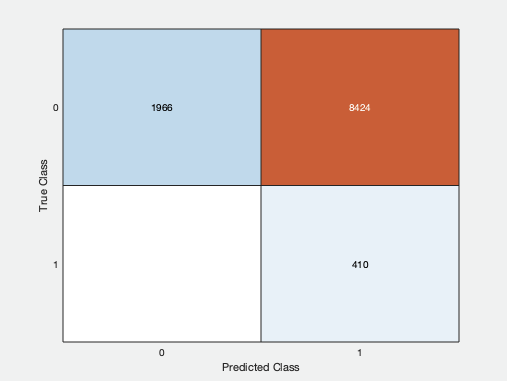
While testing different ways of finding labels and extracting features, our outputs varied in result constantly. A few of our intermediate, rather laughable, confusion matrixes are shown below that we had the displeasure to see after our program would finish. The rightmost classifying no events at all, the middle prediciting nearly every event as a braking event, and the leftmost predicting only non-braking events.

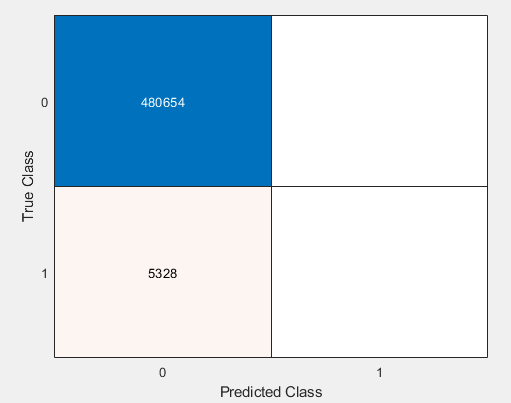
Eventually, once implementing the bottom two pieces of code listed above, our confusion matrix and ROC curve managed to output as such:

Our final confusion matrix, with a braking event recall of 92.9%, non-braking event recall of 98.2%, precision of 69.4%, and F1 score of 79.4%..

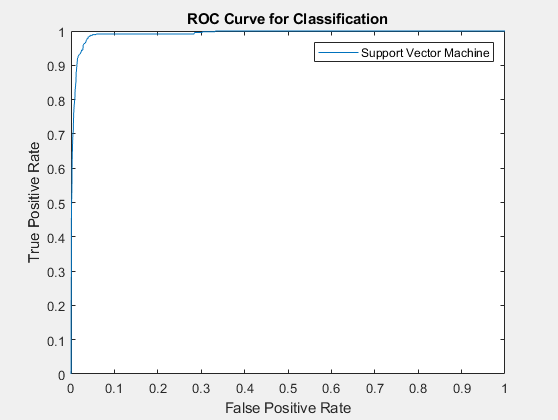
Our final ROC curve displaying the high rate of accuracy of our True Positive classification by following along the left-hand border, then the top border of the plot.

Conclusions