Team Rocket (Bryan Carvalheira, Isaac Henry, JT Palmer)

Example of a right pose from person 1

Approach/Algorithm:

We used the sum of square differences also known as SSD to get our results. The point of using SSD is that if the images being compared are matching or similar, then the SSD will be a low value. We do this on all the poses involved and on the new test images being brought in to compare. The one with the lowest SSD will in turn be the correct pose. As stated earlier, we started off using PCA, but then made a switch to LDA. While both are linear transformation techniques, we suspect that LDA should be superior for recognizing different poses.

Example SSD Code

%This is SSD used on 5 different poses
curIm = im(:);
            curImA = curIm - meanA;
            curImB = curIm - meanB;
            curImC = curIm - meanC;
            curImD = curIm - meanD;
            curImU = curIm - meanU;
            %Compute eigencoefficients of this image. This will be based on V as well as meanA that were computed in the training phase!
            eigcoeffs_imA = VA' * curImA;
            eigcoeffs_imB = VB' * curImB;
            eigcoeffs_imC = VC' * curImC;
            eigcoeffs_imD = VD' * curImD;
            eigcoeffs_imU = VU' * curImU;
        
            %For current value of k, figure out the index of the closest coefficient from the array eigcoeffs_training
            differenceA = eigcoeffs_imA(1:k) - eigcoeffs_trainingA(1:k, :);
            differenceB = eigcoeffs_imB(1:k) - eigcoeffs_trainingB(1:k, :);
            differenceC = eigcoeffs_imC(1:k) - eigcoeffs_trainingC(1:k, :);
            differenceD = eigcoeffs_imD(1:k) - eigcoeffs_trainingD(1:k, :);
            differenceU = eigcoeffs_imU(1:k) - eigcoeffs_trainingU(1:k, :);
            
            sqSumA = sum(differenceA.*differenceA, 1);
            sqSumB = sum(differenceB.*differenceB, 1);
            sqSumC = sum(differenceC.*differenceC, 1);
            sqSumD = sum(differenceD.*differenceD, 1);
            sqSumU = sum(differenceU.*differenceU, 1);
            
            %pow2 = difference .* difference;
            %squaredSum = sum(pow2, 1);
            [tmpA, indexA] = min(sqSumA);
            [tmpB, indexB] = min(sqSumB);
            [tmpC, indexC] = min(sqSumC);
            [tmpD, indexD] = min(sqSumD);
            [tmpU, indexU] = min(sqSumU);

One Eigenspace Method

We started with what we had and that was adjusting assignment 2 code to look for poses instead of faces. Assignment 2 only used one eigenspace, which we didn't initially think would cause a problem. When we put all 1,395 images into one eigenspace(thats the 93 poses with 15 people per pose), it became hard to differentiate the poses from one another as there was just too many images to look through, while also being too similar. To make this simpler for ourselves, we cut down the number of poses to 3, with a front, left, and right pose. This made our new total number of training images 279. However, even with this change, the success rate of getting the correct pose was still quite low. This is when Dr.Gill mentioned to our group that we should use multiple eigenspaces.

Multiple Eigenspaces Method

At this point, we have now made an eigenspace for three poses. As the figure on the right shows, we have our person recognition rate implemented, with a decent success rate. We also now have each pose seperated with a hit rate of their own. The rate was pretty low for each, but when combined gets to a number close to 100%. So the highest rec rate of a pose would be the ideal choice. Another change that this brought about was the recons. Now when you perform a recons, the image with the closest matching pose is reconstructed, and the images of the other 2 poses stop. A problem we encountered even with our fully constructed images was alignment. If you look closely you will be able to see shadows close to the head of the middle pose below. This is because when reconstructing the image, the head of this person was not exactly where it was in previous images.

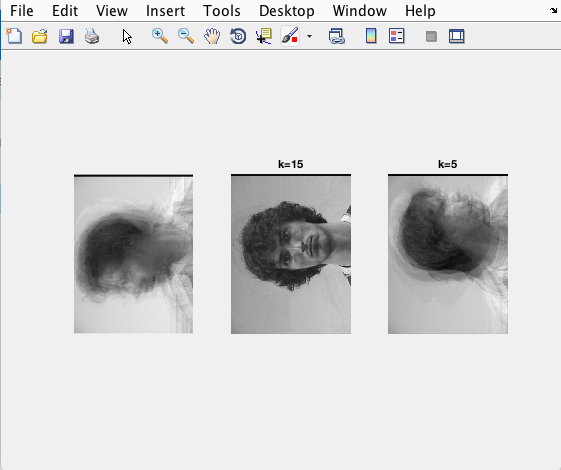
Three poses with their own eigenspace for each

When we increased to 5 poses

Example PCA Code

meanA = mean(A, 2);

%Now subtract meanA from each column of A. 
tmp = repmat(meanA, 1, N);
A = A - tmp;%One fast way to so this is to replicate meanA N times using repmat and then subtract from A. See matlab function repmat

%Compute the matrix L = A'A (where A' is the transpose of matrix A). This
%is a matrix of size N x N
L = A'*A;

[V,D] = eig(L); %Computes eigenvectors in matrix V and eigenvalues in matrix D

%Right now we have obtained eigenvectors for matrix L but we need eigenvectors for original covariance matrix C = A*A'
%Recall, if v is an eigvec of L, then Av is an eigvec of C with the same eigenvalue
%Update V.
V = A*V;
% Multiplying v by Av destroys its unit-normality property, so we divide it
% by its magnitude as below
for i=1:N 
    V(:,i) = V(:,i)/norm(V(:,i)); 
end 

% Size of V is d X N. That is total of N eigenvectors, each of size d x 1 stored column wise.
% Matlab stores eigenvectors in increasing order of eigenvalues. To make it convenient to take
% first k eigenvectors, we will reverse the order of the columns of V
V = V(:,end:-1:1); 
D = diag(D); 
D = D(end:-1:1);

% Compute eigencoefficients. 
eigcoeffs_training = V'*A;

PCA Results

After setting up PCA for the training and testing images, we had to establish a baseline. So we tested our PCA on left, right and front poses first. With K ranging from 1-45, 3 poses, and 15 different people, the highest pose recognition rate we got was 46.7% which was a right facing pose. The highest person recognition rate we got was 66.7%, slightly worse than our assignment 2. We then moved onto 5 poses, with surprising results, as recognition rate for people increased by almost 30%! Highest person recongnition rate was now up to 80%! The best pose became 40%, which was our left pose. This is interesting because the people recognition went up with more poses, however the pose recognition rate went down. After our results for PCA was completed, we switched to an LDA implementation so that we could compare and see which was better.

Example LDA Code

L = fitcdiscr(A, id, 'OptimizeHyperparameters','auto', 'DiscrimType', 'pseudolinear');

%compute the eigencoefficients for the training images.
%First compute mean should be dx1
A=A';
meanA = mean(A, 2);

%Now subtract meanA from each column of A. 
temp = repmat(meanA, 1, N);
A = A - temp;%One fast way to so this is to replicate meanA N times using repmat and then subtract from A. See matlab function repmat

%Compute the matrix L = A'A (where A' is the transpose of matrix A). This
%is a matrix of size N x N
%L = A'*A;
[V,Lambda] = eig(L.BetweenSigma, L.Sigma, 'qz'); %Computes eigenvectors in matrix V and eigenvalues in matrix D
[Lambda, sorted] = sort(diag(Lambda), 'descend');

%% Right now we have obtained eigenvectors for matrix L but we need eigenvectors for original covariance matrix C = A*A'
%Recall, if v is an eigvec of L, then Av is an eigvec of C with the same eigenvalue
%Update V.
%V = A*V;
% Multiplying v by Av destroys its unit-normality property, so we divide it
% by its magnitude as below
for i=1:N 
    V(:,i) = V(:,i)/norm(V(:,i)); 
end 

V=V(:,sorted);
% Size of V is d X N. That is total of N eigenvectors, each of size d x 1 stored column wise.
% Matlab stores eigenvectors in increasing order of eigenvalues. To make it convenient to take
% first k eigenvectors, we will reverse the order of the columns of V
%V = V(:,end:-1:1); 
%D = diag(D); 
%D = D(end:-1:1);

% Compute eigencoefficients. 
eigcoeffs_training = L.X*V;%This is multiplication of transpose of matrix V with matrix A. It is a matrix of size N x N 
eigcoeffs_training = eigcoeffs_training';

LDA Results

When doing 3 poses for LDA, we actually had our recognition rate for people go down. This was because we had to reduce the images by 85%. We did this because one of the steps used in LDA had the original images exceed the capacity of memory. Resizing them to such a small scale led to a loss of data that it becomes harder to differentiate between poses. This made our highest pose recognition rate become 33.3%, and 15.6% for people. We wanted to see how it would look if we added more poses, so we increased it back up to 5 poses. This actually made it worse again, with decresed recognition rates. We attribute this to the resizing that must occur in order to perform LDA. By losing so much data, it is harder to distinguish between the poses so it becomes harder to recognize. The best pose we got was 28%, and the best rate for people is 8%.

Conclusions